Números Decimais
Atividades de Adição e Subtração de Números Decimais
1) Observe os preços dos produtos abaixo:

a) Maria fez a compra abaixo pela internet, complete a tabela e calcule o valor a ser pago.

b) Calcule o troco considerando que Maria pagou essa compra com 3 notas de R$100,00.
2) Determine as somas de números decimais e escreva como se lê cada resultado:
a) 0,02 + 3,12 =

b) 4,54 + 2,15 =
c) 3,001 + 0,143 =
d) 75,2 + 0,01 =
e) 0,8 + 0,3 =
f) 5,4 + 2,32 =
g) 0,003 + 0,12 =
h) 0,03 + 17,8+9,2 =
i) 80,2 + 36,8 + 125,1 =
j) 58,2 + 80,6 + 120,8 =
k) 45,7 + 1,37 + 2,01 =
l) 1,5 + 2,05 + 8,13 =
3) Determine as subtrações de números decimais e escreva como se lê o resultado:
a) 49,7 - 13,2 =
b) 75,2 - 8,8 =
c) 128,3 - 1,05 =
d) 138,2 - 2,05 =
e) 4,3 - 0,8 =
f) 989,8 - 63,47 =
g) 4,35 - 3,852 =
h) 2,135 - 1,78 =
i) 9,031 - 8,35 =
Razão e Proporção
Razão

Resolução:
- número de cadeiras reservadas (17)
- número total de cadeiras (70)
Agora tente fazer as atividades abaixo:
1) (UERJ 2020) Admita que, em dezembro de 2014, uma filha tinha 20 anos e seu pai, 50.
Em dezembro de 2024, a razão entre as idades da filha e do pai será de:
A) 1/5
B) 1/2
C) 3/4
D) 4/3
A) 3/4
B) 2/3
C) 3/7
D) 2/5
E) 1/2
A → 28 quilômetros com 4 litros
B → 100 quilômetros com 14 litros
C → 60 quilômetros com 8 litros
D → 72 quilômetros com 9 litros
E → 84 quilômetros com 12 litros.
Sabendo que ele comprou o carro mais econômico, o escolhido foi?
A) A
B) B
C) C
D) D
E) E
4) Em uma sala de aula há 35 alunos, e 20 são meninas. A razão entre a quantidade de meninos e a quantidade de meninas é:
A) 4/7
B) 3/7
C) 1/2
D) 3/4
E) 4/3
5) Em um campeonato de futebol, a média de gols marcados por um time é muito importante para a análise do comportamento desse time e busca de melhorias no desempenho da equipe. Se um determinado clube marcou 12 vezes durante 20 jogos, podemos afirmar que a média de gols por partida é de:
A) 0,6 gol por partida.
B) 0,8 gol por partida.
C) 1 gol por partida.
D) 1,6 gol por partida.
E) 2 gols por partida.
6) Num exame,havia 180 candidatos,tendo sido aprovados 60,a razão entre o número de reprovados e o de aprovados é de:
a) 1/2
b) 2
c) 1/3
d) 3
7) Numa prova de Matemática,um aluno acertou 12 das 20 questões dadas.Qual é a razão do número de questões que ele acertou para o número de questões da prova?
a) 2/5
b) 3/5
c) 4/5
d) 2
8) Uma equipe de futebol apresenta o seguinte retrospecto no campeonato:
- 30 vitórias
- 18 empates
- 12 derrotas
Proporção
Os números racionais a, b, c e d são proporcionais se, e somente se, a igualdade a seguir for verdadeira.
![]()
De maneira equivalente, podemos dizer que a igualdade será verdadeira somente quando a multiplicação cruzada for verdadeira.Veja:
b . c = a . d
Como calcular proporções
Para verificar ou calcular se, de fato, os números são proporcionais, basta aplicar a primeira propriedade, caso a igualdade seja verdadeira, então os números são proporcionais. Veja os exemplos abaixo:
a)Verifique se os números 15, 30, 45 e 90 são proporcionais.
Devemos, nessa ordem, montar as razões e, em seguida, realizar a multiplicação cruzada.
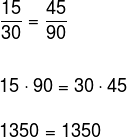
Conclusão: Como deu uma igualdade,os números nesta ordem formam uma proporção.
b) Os números 2, 4, x e 32 são proporcionais. Determine o valor de x.
Como afirmamos que os números, na ordem que foram apresentados, são proporcionais, logo, podemos igualar as razões entre eles e aplicar a propriedade fundamental, veja:

Exercício 1) Verifique se os números abaixo na ordem que eles aparecem são proporcionais:
a) 3 , 4 , 6 e 8
b) 4 , 8 , 10 e 20
c ) 7 , 3 , 49 e 21
d) 4 , 6 , 20 e 30
e) 8 , 9 , 10 e 15
f) 12 , 15 , 10 e 13
Exercício 2) Os números abaixo na ordem que eles aparecem são proporcionais,determine o valor de x:
a) 
b) .jpg)
c) .jpg)
Exercício 3) Uma criança de 1 m de altura projeta uma sombra de 0,5 m. No mesmo instante,um edifício de 18 m irá projetar uma sombra de :
a) 6 m
b) 8 m
c) 9 m
d) 12 m
Exercício 4) Uma fotografia tem 10 cm de largura e 15 cm de comprimento.Queremos ampliá-la de modo que seu comprimento tenha 18 cm.Então,na foto maior,a largura medirá:
a) 12 cm
b) 13 cm
c) 14 cm
d) 16 cm
Juros Simples
Podemos definir juros como o rendimento de uma aplicação financeira, valor referente ao atraso no pagamento de uma prestação ou a quantia paga pelo empréstimo de um capital. Atualmente, o sistema financeiro utiliza o regime de juros compostos, por ser mais lucrativo. Os juros simples eram utilizados nas situações de curto prazo, hoje ele não faz mais parte do mercado financeiro, mas vamos entender como ele é calculado.
Fórmula matemática para o cálculo de Juros Simples
J = C . i . n
J : Juros simples
i : Taxa de Juros (sempre na forma unitária)
n : número de período de tempo
Duas considerações importantes nos cálculos:
Taxas equivalentes em Juros Simples
- 1 ano comercial tem 360 dias;
- 1 ano tem 12 meses;
- 1 mês tem 30 dias.
Como calcular Juros Simples
J = C . i . n
- Note que o período da taxa ( i ) e do período de tempo ( n ) não estão em sintonia.Mais conveniente neste problema é transformar 90 dias em 3 meses.
- E a taxa sempre deve estar na forma unitária.
J = C . i . n
1) Determinar o juro produzido por R$ 50000,00, quando aplicados a 2% am, em 8 meses.
a) R$6000,00
b) R$7000,00
c) R$8000,00
d) R$9000,00
2) César aplicou R$ 2.000,00, durante um ano, à taxa de 6 % ao mês. Qual o juro recebido por ele?
a) R$1000,00
b) R$1440,00
c) R$2000,00
d) R$2300,00
3) Júlio emprestou R$ 5.000,00 de um amigo por cinco meses, a uma taxa de juros simples de 4% ao mês. Quanto deverá pagar de juros para saldar a dívida?
4) Um capital de R$ 10.000,00 é aplicado à taxa de 5% ao ano. Quanto esse valor renderá de juros simples, durante 36 meses?
a) R$ 800,00
b) R$ 1.200,00
c) R$ 1.500,00
d) R$ 3.300,00
a) R$ 300,00
b) R$ 320,00
c) R$ 350,00
d) R$ 375,00
6) Calcule o juro produzido por R$ 20000,00, em 36 meses, a uma taxa de 12% ao ano.
a) R$7200,00
b) R$8200,00
c) R$9200,00
d) R$9500,00
7)Calcule o juro produzido por R$ 10 000, 00, em 3 meses, a 0, 02% ao dia.
a) R$72,00
b) R$89,00
c) R$180,00
d) R$200,00
8) Calcule o juro produzido por R$ 20 000, 00, em 3 anos, a 12% ao ano.
a) R$6200,00
b) R$7200,00
c) R$8200,00
d) R$9200,00
9) Calcule o juro produzido por R$ 5 000, 00, em 2 anos, a 2, 5% ao mês.
a) R$1200,00
b) R$3000,00
c) R$3200,00
d) R$3700,00
a) R$5 200,00
b) R$5 300,00
c) R$5 875,00
d) R$6 700,00
11) Calcule o juro produzido por R$ 2 000, 00, em 4 meses, a 2% ao mês.
a) R$100,00
b) R$160,00
c) R$175,00
d) R$180,00
********Cálculo do Capital (C)********
Exemplo:Um capital foi aplicado a juro simples com taxa de 10% ao mês, durante
cinco meses. Se no fim desse período o juro produzido foi de R$ 305.
Qual foi o capital aplicado?
Dados: C=?
J=305
i=10% am = 0,1 am
n=5 meses
a) 500,00
b) 600,00
c) 390,00
d) 610,00
Exercícios:
1) Calcule o capital que, em 5 anos, a 25% a.a, rendeu R$ 5 000, 00 de juro.
a) 2000,00
b) 2600,00
c) 3100,00
d) 4000,00
a) 10 000,00
b) 12 000,00
c) 13 000,00
d) 14 000,00
3) Determine o capital que produz um juros simples de R$8 000,00 à uma taxa de 2% am em 8 meses?
a) 50000,00
b) 52000,00
c) 53000,00
d) 54000,00
4) Uma aplicação rende de juros simples R$1 500,00 aplicado a uma taxa de 5% aa durante 36 meses.Então o capital aplicado foi:
a) 1 000,00
b) 10 000,00
c) 15 000,00
d) 18 000,00
5) Calcule o capital que em 4 meses aplicado em uma taxa de 2% am rendeu R$160,00 reais de juros simples.
a) 2 000,00
b) 5 000,00
c) 6 000,00
d) 7 000,00
********Cálculo do Tempo (n)********
1) Um capital de 4000 reais aplicados a 25% a.a, rendeu 5000 reais de juro.Determine quanto tempo foi aplicado.
a) 2 anos
b) 3 anos
c) 4 anos
d) 5 anos
2) Calcule o tempo que um capital de R$ 2 000,00 deve ser aplicado a uma taxa de 2% ao mês para render de juros R$160,00.
a) 2 meses
b) 3 meses
c) 4 meses
d) 5 meses
********Cálculo da Taxa (i)********
Porcentagem de Porcentagem
O quintal de uma casa corresponde a 30% da área do terreno e uma piscina será construída ocupando 60% deste quintal. Qual a porcentagem de área que a piscina ocupará em relação ao terreno?
Resposta : A área da piscina corresponde a 18% da área do terreno.
a) 40% de 50%=
b) 25% de 30%=
c) 12% de 40%=
d) 45% de 60%=
e) 10% de 55%=
Porcentagem em figuras
Observe a porcentagem que corresponde a parte colorida das figuras abaixo:
Exercício: Qual a porcentagem referente a parte colorida de cada figura abaixo:
Como calcular a Variação Percentual
Variação Percentual
Podemos dizer que variação percentual é uma forma de apresentar a relação entre dois números na forma percentual.
Por exemplo, um produto que custava R$10 aumentou para R$12, Qual foi a variação percentual de aumento?
Se subiu de 10 para 12, ele teve uma variação percentual de 20% ou seja uma variação percentual de aumento , por uma questão de praticidade iremos usar a sigla VPA.
Por outro lado, digamos que um outro produto custava R$20 baixou a R$10.
Este é um caso inverso ao anterior.
Neste caso temos uma redução de 50%, ou seja uma variação percentual de redução, por uma questão de praticidade iremos usar a sigla VPR.
Cálculo da Variação Percentual
1º caso: Fórmula matemática para o cálculo da Variação Percentual de aumento (VPA)
Atenção:O resultado obtido devemos multiplicar por 100 para podermos colocar o símbolo de %.
Exemplo de aplicação:
- Aplicando a fórmula acima, temos:
Não esqueça! O resultado obtido devemos multiplicar por 100 para podermos colocar o símbolo de %.

































