Vídeo aula e exercícios de Progressão Geométrica-P.G.

EXERCÍCIOS:

1)Dada a PG (2,4,8,... ), pede-se calcular o décimo termo.
Resp:a10 = 1024
2) Sabe-se que o quarto termo de uma PG crescente é igual a 20 e o oitavo termo é igual a 320. Qual a razão desta PG?
Resp: q=2
3)O 5º termo da P.G.(2;4;8;16;...) é:
a) 16
b) 32
c) 12
d) 52

Vídeo-aula e exercícios de Progressão Aritmética (P.A.)

Exercícios:

1.A soma dos 20 elementos iniciais da P.A. (-10,-6,-2,2,...) é:
a) 660 b) 640 c) 600 d) 560 e) 540

2.A soma dos 40 elementos iniciais da P.A. (3,9,15...) é:
a) 4500 b) 4640 c) 5600 d) 4800 e) 540

3-Calcule a soma dos 50 primeiros termos da PA(2, 6, 10,...).
a)5000 b)5300 c)5400 d)5800 e)6000

4-O vigésimo termo da Progressão Aritmética ( 3, 8, 13, 18 ...)é:
a) 63 b) 74 c) 87 d) 98 e) 104

5-Um ciclista percorre 20 km na primeira hora, 17 km na segunda hora, e assim por diante, em progressão aritmética. Quantos quilômetros percorrerá em 5 horas?
a)50km b)60km c)70km d)80km e)90km

Plano Cartesiano

O plano cartesiano foi criado por René Descartes vamos conhecer uma parte da sua biografia(publicada pelo UOL educação).

Descartes, por vezes chamado de o fundador da filosofia moderna e o pai da matemática moderna, é considerado um dos pensadores mais influentes da história humana.

Nasceu em La Haye, a cerca de 300 quilômetros de Paris. Seu pai, Joachim Descartes, advogado e juiz, possuía terras e o título de escudeiro, além de ser conselheiro no Parlamento de Rennes, na Bretanha.

Com um ano de idade, Descartes perdeu a mãe, Jeanne Brochard, no seu terceiro parto, e foi criado pela avó. Seu pai se casou novamente e chamava o filho de "pequeno filósofo". Mais tarde, aborreceu-se com ele quando não quis exercer o direito, curso que concluiu na universidade de Poitiers em 1616.

Em 1618, Descartes foi para a Holanda e se alistou no exército de Maurício de Nassau. A escola militar era, para ele, uma complementação da sua educação. Nessa época fez amizade com o duque filósofo, doutor e físico Isaac Beeckman, e a ele dedicou o "Compendium Musicae", um pequeno tratado sobre música.

Em 1619, viajou para a Dinamarca, Polônia e Alemanha, onde, segundo a tradição, no dia 10 de novembro, teve uma visão em sonho de um novo sistema matemático e científico. Três anos depois retornou a França e passou os anos seguintes em Paris e em outras partes da Europa.

Em 1628, Descartes, incentivado pelo cardeal De Bérulle, escreveu "Regras para a Direção do Espírito". Buscando tranqüilidade, partiu para os Países Baixos, onde viveu até 1649.

Em 1629 começou a trabalhar em "Tratado do Mundo", uma obra de física. Mas em 1633, quando Galileu foi condenado pela igreja católica, Descartes não quis publicá-lo. Em 1635 nasceu sua filha ilegítima, Francine, que morreria em 1640.

Em 1637, publicou anonimamente "Discurso sobre o Método para Bem Conduzir a Razão a Buscar a Verdade Através da Ciência". Os três apêndices desta obra foram "A Dióptrica" (um trabalho sobre ótica), "Os Meteoros" (sobre meteorologia), e "A Geometria" (onde introduz o sistema de coordenadas que ficaria conhecido como "cartesianas", em sua homenagem). Seu nome e suas teorias se tornaram conhecidos nos círculos ilustrados e sua afirmação "Penso, logo existo" (Cogito, ergo sum) tornou-se popular.

Em 1641, surgiu sua obra mais conhecida: as "Meditações Sobre a Filosofia Primeira", com os primeiros seis conjuntos de "Objeções e Respostas". Os autores das objeções foram Johan de Kater; Mersene; Thomas Hobbes; Arnauld e Gassendi. A segunda edição das Meditações incluía uma sétima objeção, feita pelo jesuíta Pierre Bourdin..

Em 1643, a filosofia cartesiana foi condenada pela Universidade de Utrecht (Holanda) e, acusado de ateísmo, Descartes obteve a proteção do Príncipe de Orange. No ano seguinte, lançou "Princípios de Filosofia", um livro em grande parte dedicado à física, o qual ofereceu à princesa Elizabete da Boêmia, com quem mantinha correspondência.

Uma cópia manuscrita do "Tratado das Paixões" foi enviada para a rainha Cristina da Suécia, através do embaixador francês. Frente a insistentes convites, Descartes foi para Estocolmo em 1649, com o objetivo de instruir a rainha de 23 anos em matemática e filosofia.O horário da aula era às cinco horas da manhã. No clima rigoroso, sua saúde deteriorou. Em fevereiro de 1650, ele contraiu pneumonia e, dez dias depois, morreu.

Em 1667, depois de sua morte, a Igreja Católica Romana colocou suas obras no Índice de Livros Proibidos.

O plano cartesiano consiste em dois eixos perpendiculares, sendo o horizontal chamado de eixo das abscissas e o vertical de eixo das ordenadas. O plano cartesiano foi desenvolvido por Descartes no intuito de localizar pontos num determinado espaço. As disposições dos eixos no plano formam quatro quadrantes, mostrados na figura a seguir:

O encontro dos eixos é chamado de origem. Cada ponto do plano cartesiano é formado por um par ordenado (x ;y ), onde x: abscissa e y: ordenada.

O sistema de coordenadas cartesianas possui inúmeras aplicações, desde a construção de um simples gráfico até os trabalhos relacionados à cartografia, localizações geográficas, pontos estratégicos de bases militares, localizações no espaço aéreo, terrestre e marítimo.
Observe abaixo as atividades de pontos no plano cartesiano,feita pelos alunos Samuel,Pablo e Fernando:

 Marque os pontos cujas coordenadas são dadas abaixo e ligue-os em ordem alfabética com segmentos de reta. 

1ª atividade:

A (8 , 1) B (1 , 8) C (1 , 11) D (3 , 13) E (6 , 13) F (8 , 11) G (10 , 13)

H (13 , 13) I (15 , 11) J (15 ,8) (não esqueça de ligar J com A.)

2ª atividade:

A(0 , 8) B(0 , 12) C(3 , 15) D(5 , 15) E(5 , 14) F(3 , 12) G(2 , 12) H(2 , 9)

I(4 , 11) J(6 , 11) K(8 , 9) L(8 , 13) M(10 , 11) N(14 , 11) O(16 , 13)

P(16 , 7) Q(15 , 6) R(13 , 5) S(11 , 5) T(9 , 6) U(8 , 7) V(8 , 4) W(9 , 4) X(9 , 2) Y(6 , 2) Z(6 , 6) Z1(4 , 6) Z2(3 , 5) Z3(3 , 4) Z4(5 , 4) Z5(5 , 2) Z6(1 , 2) (ligue em ordem alfabética e não esqueça de ligar os pontos Z6 com A.)

•Comece novamente no mesmo plano cartesiano:

A(9 , 8) B(9 , 10) C(11 , 10) D(11 , 8) (ligue em ordem alfabética e não esqueça de ligar os pontos D com A.)

•Comece novamente no mesmo plano cartesiano:

A(13 , 10) B(15 , 10) C(15 , 8) D(13 , 8) (ligue em ordem alfabética e não esqueça de ligar os pontos D com A.)

•Comece novamente no mesmo plano cartesiano:

A(11 , 7) B(12 , 8) C(13 , 7) (ligue em ordem alfabética e não esqueça de ligar os pontos C com A.)

                 

3ª atividade:

Marque os pontos cujas coordenadas são dadas abaixo e ligue-os com segmentos de reta. Surgirá um desenho no plano cartesiano que você poderá colorir. A cada símbolo # , recomece a sequência . Desvende esse mistério!

# (1 , 1 ) (1 , 4 ) (2 , 5 ) (5 , 5 ) (6 , 4 ) (6 , 1 ) (5 , 0 ) (2 , 0 ) (1 , 1 )
# (0 , 2 ) (0 , 6 ) (1 , 7 ) (11 , 7 ) (11 , 8 ) (12 , 8 ) (12 , 7 ) (15 , 7 ) (16 , 6 ) (16 , 2 ) 
# (0 , 4 ) (2 , 6 ) (5 , 6 ) (7 , 4 ) (7 , 2 ) (9 , 2 ) (9 , 4 ) (11 , 6 ) (14 , 6 ) (16 , 4 )
# (10 , 1 ) (10 , 4 ) (11 , 5 ) (14 , 5 ) (15 , 4 ) (15 , 1 ) (14 , 0 ) (11 , 0 ) (10 , 1 )
# (6 , 7 ) (8 , 10 )
# (2 , 3 ) (3 , 4 ) (4 , 4 ) (5 , 3 ) (5 , 2 ) (4 , 1 ) (3 , 1 ) (2 , 2 ) (2 , 3 ) 
# (12 , 1 ) (11 , 2 ) (11 , 3 ) (12 , 4 ) (13 , 4 ) (14 , 3 ) (14 , 2 ) (13 , 1 ) (12 , 1 )

4ª atividade:

 Marque os pontos cujas coordenadas são dadas abaixo e ligue-os com segmentos de reta. Surgirá um desenho no plano cartesiano que você poderá colorir. A cada símbolo # , recomece a sequência . Desvende esse mistério! 

# (0 , 10) (2 , 11) (0 , 12) (2 , 12) (2 , 14) (3 , 15) (7 , 15) (9 , 13) (9 , 11) (6 , 9) (6 , 8) (10 , 8) (12 , 11)

 (14 , 11) (13 , 8) (16 , 9) (16 , 7) (14 , 5) (16 , 6) (16 , 3) (13 , 0) (3 , 0) (0 , 3) (0 , 7) (3 , 9) (3 , 10) (0 , 10) 

# (3 , 11) (3 , 13) (5 , 13) (5 , 11) (3 , 11) 

# (4 , 13) (4 , 12) (3 , 12) 

# (8 , 7) (3 , 6) (2 , 5) (2 , 3) (5 , 1) (11 , 1) (14 , 4) (12 , 5) (9 , 3) (13 , 7) (11 , 7) (7 , 4) (8 , 6) (8 , 7)

5ª atividade:

Máximo Divisor Comum(M.D.C)

• CÁLCULO DO M.D.C. POR DECOMPOSIÇÃO EM FATORES PRIMOS

• CÁLCULO DO M.D.C. PELO PROCESSO DAS DIVISÕES SUCESSIVAS

Nesse processo efetuamos várias divisões até chegar a uma divisão exata. O divisor desta divisão é o m.d.c. Acompanhe o cálculo do m.d.c.(48,30).

Regra prática:

1º) dividimos o número maior pelo número menor;

48 / 30 = 1 (com resto 18)

2º) dividimos o divisor 30, que é divisor da divisão anterior, por 18, que é o resto da divisão anterior, e assim sucessivamente;

30 / 18 = 1 (com resto 12)

18 / 12 = 1 (com resto 6)

12 / 6 = 2 (com resto zero - divisão exata)

3º) O divisor da divisão exata é 6. Então m.d.c.(48,30) = 6.

• NÚMEROS PRIMOS ENTRE SI

Dois ou mais números são primos entre si quando o máximo

divisor comum é 1.

Exemplos:

Os números 35 e 24 são números primos entre si, pois mdc (35,24) = 1.

Os números 35 e 21 não são números primos entre si, pois mdc (35,21) = 7.

• PROPRIEDADE DO M.D.C.

Dentre os números 6, 18 e 30, o número 6 é divisor dos outros dois. Neste caso, 6 é o m.d.c.(6,18,30). Observe:

6 = 2 x 3

18 = 2 x 3 x 2

30 = 2 x 3 x 5

Portanto m.d.c.(6,18,30) = 6

Dados dois ou mais números, se um deles é divisor de todos os outros, então

ele é o m.d.c. dos números dados.

Exercício 1)

a) Qual o MDC de 12 e 18?
b) Calcule o MDC de 24 e 36.
c) Encontre o MDC de 15 e 25.
d) Determine o MDC de 48 e 60.
e) Qual o MDC de 16, 24 e 32?
f) Calcule o MDC de 21, 35 e 49.
g) Encontre o MDC de 30, 45 e 60.
h) Determine o MDC de 14, 28 e 42.
i) Qual o MDC de 18, 36 e 54?
j) Calcule o MDC de 20, 30 e 50.

Exercício 2)

Calculadora MDC

Número 1: Número 2: Número 3: Número 4:

A Divina proporção

Na natureza, a razão áurea parece orientar a posição das pétalas e sementes nas margaridas e girassóis, e a curvatura da concha do Náutilus. A divina proporção também foi encontrada na seqüência de Fibonacci.

Nas artes, retângulos áureos serviram de moldura para inúmeras obras, para artistas como Leonardo da Vinci e Albrecht Dührer. Para além da harmonia, a razão áurea era um ideal de perfeição.
Segundo o modelo do homem perfeito, impresso no Homem Vitruviano, de Da Vinci, as dimensões obedecem a divina proporção; o umbigo divide a altura do corpo humano em dois segmentos que estão na razão áurea.

O ombro divide a distância entre as extremidades dos dedos (braços abertos

perpendicularmente ao corpo) em dois segmentos que estão na mesma razão áurea.

Dízimas periódicas Simples e Composta

As dízimas periódicas são números decimais periódicos, ou seja, apresentam um ou mais algarismos que se repetem na mesma ordem infinitamente. O algarismo que se repete é chamado de período.
Os números decimais periódicos pertencem ao conjunto dos números racionais, pois podem ser escritos na forma de fração. 
Quando um número é decimal infinito, mas não apresenta algarismos que se repetem, ou seja, não possui um período, ele não será uma dízima periódica e sim um número irracional.
Existe dois tipos de dízimas periódicas, vamos conhecer a primeira:

Dízima periódica simples

Dízima periódica simples é quando analisamos a parte decimal (parte depois da vírgula) e observamos que antes do período não aparece nenhum número diferente dele. Veja os exemplos:

a)1,4444... ( analisando a parte decimal podemos notar que antes do período 4,não aparece nenhum número diferente dele).

b)3,7777... ( analisando a parte decimal podemos notar que antes do período 7,não aparece nenhum número diferente dele).

Dízima periódica composta

Dízima periódica composta é quando analisamos a parte decimal (parte depois da vírgula) e observamos que antes do período aparece um número que é diferente dele. Veja os exemplos:

a)4,27777... (analisando a parte decimal podemos notar que antes do período 7 aparece um número diferente, no caso o número 2).

b)0,25323232... (analisando a parte decimal podemos notar que antes do período 32 aparece um número diferente, no caso o número 25).

 

Representação das dízimas periódicas

As dízimas podem estar escritas na forma de fração geratriz ou na forma de número decimal. Quando estiver escrita na forma decimal, colocamos três pontinhos no final para indicar que os algarismos se repetem infinitamente. Podemos ainda representar esse tipo de número colocando um traço horizontal apenas em cima do seu período.
Exemplos:

COMO SABER SE UMA DÍZIMA PERIÓDICA É SIMPLES OU COMPOSTA 

Exercício : Classifique em Dízima Periódica Simples ou Dízima Periódica Composta

a) 2,7777.... ►

b) 5,24444.... ►

c) 9,22222.... ►

d) 25,128888...►

e) 8,525252... ►

FRAÇÃO GERATRIZ DE UMA DÍZIMA PERIÓDICA

É possível determinar a fração que deu origem a uma dízima periódica.

Denominamos esta fração de geratriz da dízima periódica.

Assista a aula do Prof. Nivaldo Galvão e aprenda a encontrar a fração geratriz de um dízima periódica simples e composta.

 

EXERCÍCIOS

1) Analise a fração a seguir:

Podemos afirmar que ela é a fração geratriz da dízima:

A) 2,77…

B) 0,62626262…

C) 2,55…

D) 0,2666…

E) 0,27272727…

2) Seja x = 1,123123… A diferença entre o numerador e o denominador da sua representação fracionária é:

A) 123.

B) 999.

C) 321.

D) 112.

E)1122.

3) A fração geratriz de dízima periódica 3,151515… é igual a:

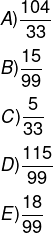
4) A fração geratriz da dízima 15,2222… é ?

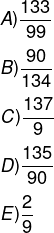
5) Assinale a alternativa que corresponde a fração geratriz da dízima periódica 2,5303030... 

a) 25/ 99

b) 37/ 9

c) 135/999

d) 267/990

e) 167/66

As Probabilidades e os Jogos de azar

O amadurecimento das técnicas combinatórias em probabilidades

 

Até então as técnicas de enumeração das possibilidades favoráveis num evento aleatório eram simplórias e restritas a casos numéricos. Para que se pudesse tratar de problemas envolvendo muitas possibilidades ou eventos de natureza genérica, precisava-se técnicas mais apuradas do que as que empregaram Cardano e Tartaglia. A principal deficiência técnica desses italianos era a precariedade de sua notação, a qual não tinha como tratar de casos genéricos. Essa capacidade só foi atingida com o Cálculo Literal ( Logística Speciosa ) de François Viète c. 1 600 e com a álgebra desenvolvida por Descartes em sua La Géometrie c. 1630. Consequentemente, não deve vir como surpresa que é só na metade do século dos 1600's que aparecem as condições para a abordagem de problemas gerais de probabilidades. Isso coube a dois outros franceses: Fermat e Pascal.

Em 1 654, um famoso jogador profissional, Antoine Gombauld, autodenomidado o Cavaleiro de Méré, escreveu uma carta ao famoso matemático francês Blaise Pascal, propondo-lhe resolver alguns problemas matemáticos que tinha encontrado em suas lides com jogos de azar.

Entre os problemas propostos por de Méré estava o seguinte:

Jogando com um par de dados honestos, quantos lances são necessários para que tenhamos uma chance favorável ( ou seja, de mais de 50% ) de obtermos um duplo-seis, ao menos uma vez?

O interesse de de Méré no problema residia no fato de que sua "solução" para o mesmo não funcionava na prática, produzindo-lhe constantes prejuízos.

Com efeito, ele não conseguia ver o que estava errado em seu raciocínio:

" Quando jogamos apenas um dado, temos chance 1/6 de obter um seis, e como 3 x 1/6 = 50% e 4 x 1/6 = 67%, vemos que precisamos jogá-lo 4 vezes para ter chance maior do que 50% de obtermos, ao menos uma vez, um seis. Ora, quando jogamos um par de dados temos 36 possibilidades, ou seja 6 vezes mais possibilidades de quando jogamos um único dado, consequentemente, precisaremos jogar o par de dados 6 x 4 = 24 vezes para ter chance maior do que 50% de obtermos, ao menos uma vez, um duplo seis".

Pascal percebeu o erro de de Méré e se dispôs a achar a solução correta. Trocando idéias com o grande matemático Fermat, logo se convenceram que a resolução teria de passar pela enumeração combinatorial das possibilidades de ocorrência do duplo-seis. Procurando uma maneira inteligente de fazer essa trabalhosa enumeração, acabaram dando plena maturidade às técnicas introduzidas por Cardano e Tartaglia:

• Fermat redescobriu e aperfeiçou a técnica de Cardano, baseando o cálculo de probabilidades no cálculo combinatório, bem ao estilo que hoje empregamos rotineiramente.

• Pascal seguiu um caminho menos importante, redescobriu e aperfeiçou a técnica de Tartaglia que baseava-se no uso do que hoje, no Brasil e vários outros lugares, chama-se de triângulo aritmético de Pascal ( na Itália, o triângulo aritmético é chamado de triângulo de Tartaglia, mas a verdade é que o triângulo aritmético já era conhecido há séculos pelos indianos, chineses e pelos islamitas )

Dessa maneira, conseguiram mostrar, cada um à sua maneira, que:

• em 24 lances de um par de dados, a probabilidade de ocorrer, ao menos uma vez, um duplo-seis é de 49.1%

( sendo então, ao contrário do que achava de Méré, "desfavorável" ao jogador )

• em 25 lances de um par de dados, a probabilidade de ocorrer, ao menos uma vez, um duplo-seis é de 50.6%

( sendo, agora, "favorável" ao jogador )

Pascal e Fermat são os primeiros a resolverem problemas genéricos, não numéricos. Por exemplo, Pascal resolveu a seguinte versão genérica do Problema dos Pontos de Pacioli:

"jogo terminaria quando um jogador fizesse m+n pontos, mas precisou ser interrompido quando um deles tinha m pontos e o outro tinha n pontos; como dividir os prêmios?"
Contudo, nem Pascal e nem Fermat chegaram a tratar de teoremas de probabilidades.

As Probabilidades Matemáticas no mais famoso jogo de azar do Brasil

A MEGA SENA é o jogo de azar mais famoso do Brasil, na vídeoaula o Prof.Nivaldo Galvão mostra como é mínima a chance de um apostador acertar com um jogo simples as 6 dezenas sorteadas.

Programa da calculadora HP-12C para calcular Taxas Equivalentes em Juros Compostos

Abaixo apresentamos um programa para você colocar na sua HP-12C para calcular a taxa equivalente em qualquer período,isto é,conhecida uma taxa e seu período pode-se calcular sua equivalente num determinado período.

Observação a tecla xy (da programação abaixo) é a que fica ao lado  da tecla CLX.

Os dois primeiros exemplos da videoaula do Prof.Nivaldo Galvão na HP-12C com o uso da programação fica assim:

✔ Transformando taxa mensal em taxa anual:

✔ Transformando taxa anual em taxa mensal:

Aplicações da Função do 1ºgrau

1- Um vendedor recebe mensalmente um salário composto de duas partes: uma parte fixa, no valor de R$ 300,00, e uma parte variável, que corresponde a uma comissão de 8% do total de vendas que ele fez durante o mês.

a) Expressar a função que representa seu salário mensal (Sm):

b) Calcular o valor do salário do vendedor sabendo que durante um mês ele ganha R$ 10 000,00 em produtos.

2- O preço a pagar por uma corrida de táxi depende da distância percorrida. A tarifa y é composta de duas partes: uma parte fixa chamada bandeirada e uma parte variável que depende do número x de quilômetros rodados. Suponha que a bandeirante esteja custando R$ 2,00 e o quilômetro rodado, R$ 0,50.

a) Expresse y em função de x:

b) Quanto se pagará por uma corrida em que o táxi rodou 11Km?

3- Faça no plano cartesiano o esboço do gráfico da função y = 3x – 2:

4- Determine as funções relativa a cada reta no plano cartesiano abaixo:

Operações com radicais e uma aplicação na Geometria Espacial

Exercícios proposto referente a vídeo aula do Prof.Nivaldo Galvão

1)Simplifique os radicais:

√90=

√27 + √243 + 2√3=

2)Calcular a diagonal de um paralelepípedo retângulo cujas dimensões são 4 cm,3 cm e 12 cm.

3)A diagonal de um paralelepípedo retângulo mede 5√2 m. Sabendo que duas de suas arestas medem 3m e 5m,calcule a medida da aresta desconhecida.

Equivalência de Capitais no sistema de capitalização composta

A equivalência de capitais é bastante utilizada na renegociação de dívidas,em particular,na substituição de um conjunto de títulos por outro,equivalente ao primeiro.

• A importância da data focal
  

Do ponto de vista teórico,a escolha da data focal é indiferente,mas do ponto de vista prático é mais conveniente escolher uma data focal que facilite o máximo o trabalho do cálculo.

Dependendo da data focal escolhida,um determinado capital poderá ser movimentado para frente ou para trás em relação ao eixo dos tempos.Portanto se quisermos levar o capital para frente,devemos multiplicá-lo pelo fator (1 + i)^n .Se quisermos levar o capital para trás.devemos dividi-lo por (1+ i)^n.

Curiosidades Numéricas-Os três prédios mais altos de São Paulo

Você sabe quais são os 3 edifícios mais altos de São Paulo? 

1º Lugar : Edifício Mirante de São Paulo com 170m de altura,localizado em frente ao viaduto Santa Efigênia desde 1960.

2ºLugar:Edifício Itália cujo nome oficial é Circolo Italiano com 165m de altura,localizado na Av.Ipiranga desde 1965.

3ºlugar: Edifício Altino Arantes mais conhecido como Edifício do Banespa inaugurado em 1947 com altura de 161m ,durante mais de 10 anos foi o mais alto de São Paulo até ser superado pelo Mirante.

A Matemática das Bicicletas

Cada pedalada de um ciclista corresponde há uma distância equivalente ao comprimento da circunferência da roda dianteira, o que justifica o fato de os primeiros modelos terem uma enorme roda dianteira. Tal mecanismo, além de exigir muito esforço do ciclista, possuía limitações para o aumento de rendimento, uma vez que o raio da roda dianteira não poderia ser maior que o comprimento da perna do ciclista.O mecanismo de transmissão usado hoje em dia para melhorar o rendimento consiste em um conjunto de duas rodas dentadas ,uma delas fixa, com pinhão livre na roda traseira, que giram sob o comando de uma corrente.As rodas possuem número diferentes de dentes, por exemplo, 14 e 42. Como o pedal está acoplado à roda dentada maior, cada volta do pedal (um giro de 42 dentes) implica três voltas da roda dentada menor já que 3.14=42. Como a roda dentada menor é a responsável por transmitir o movimento ao conjunto, podemos dizer que a bicicleta avaliada avançará uma distância igual a três vezes o comprimento da sua roda traseira para cada pedalada completa.O comprimento da circunferência C de raio r (r é a metade do diâmetro) é calculado pela fórmula C=2. pi . r (para pi o valor aproximado 3,14)e sabendo que as rodas de uma bicicleta comum têm aproximadamente 70cm ou 0,70m de diâmetro, cada pedalada implica um deslocamento de 3 vezes o comprimento da circunferência da roda,ou seja,3 . 2 . 3,14 . 0,35=6,59m. Lembrando meus queridos que r é a metade do diâmetro da roda,como a roda tem aproximadamente 0,70m,logo metade é 0,35.
Um abraço meus queridos!!!

Prof.Nivaldo Galvão